Should I add one more (or two) Dicewords?
So, after I decided that Dicewords make good sense, I decided that for my feeble brain, I could manage to memorize N dice words, rather than more, and that I could live with the possibility that someone might care enough about me to take Y-some years to crack my data. It would be astonishing if I were even on Earth that much longer!
So by now the N words that the dice provided to me are automatic. Would I gain anything worthwhile by adding one more word to my current list? It should be pretty easy to take my automatic entry for my current N words and add one more to the list and have an N+1 word list, but then I also read that I should pick such a password and then never change it.
(See how cagey I tired to be about my current system?)
Comments
-
Good question, @hawkmoth. Ultimately only you can decide what length of Diceware password you're comfortable with, but we provided a chart in our "1Password is Ready for John the Ripper" blog post which may help:
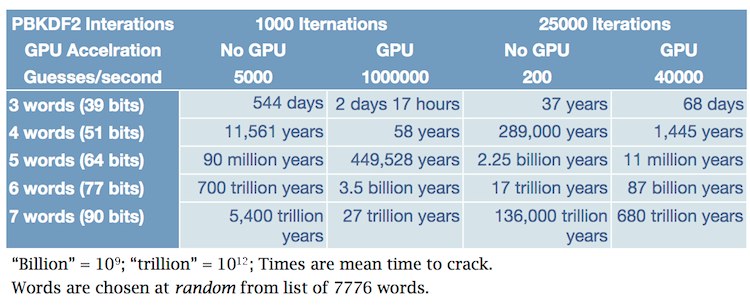
From the table you should surmise that three-word-long passwords of this sort aren’t long enough to withstand a plausible attack. You should also be able to see that anything over five words long is overkill. Or, given a Master Password with more than about 55 bits of real entropy (not the false reports that you get from most websites pretend to calculate password strength), you should be fine against any plausible attack for a long time to come.
The other part of your question is about changing your Master Password. While we do say that a Master Password is for life, there are a couple reasons that you would want to change it: if it is used elsewhere and if it is weak and needs to be made stronger.
I hope that helps you make an educated decision. Please let me know if you have any other questions or concerns. It is great that you are thinking about this.
0 -
Thanks - that table was part of how your site persuaded me that Diceware was the way to go. To me, the answer is obvious between three and four words. It's less clear as a practical matter from there to five words. I'd say that for practical purposes, four words are enough, but I was really asking for a professional assessment of that view..
0 -
It's less clear as a practical matter from there to five words. I'd say that for practical purposes, four words are enough…
I would agree with that assessment. :)
0 -
Here is one professional’s view:
The great thing about Diceware is that we know exactly how secure it is even assuming that the attacker knows the system used. … The bad news is that we need passwords that are at least five or six Dicewords long to resist plausible attacks.
Jeff wrote those words over two years ago, and the crackers haven’t been sleeping in the interim.
Arnold Reinhold, the inventor of Diceware, recommends five words (for most users) in his FAQ, which was most recently updated in April of 2012.
0 -
@benfdc, I think I once read that too, now that I look it over again.
Maybe I'm too cavalier about this, but I have trouble believing I have information that is so valuable that someone would exert the required computing power to break in to particular data. Another rather practical issue for me is that getting too long severely compromises my ability (willingness?) to get at my data on iOS devices, particularly the iPhone. Yes, I realize that those devices are the ones in the world where they and their enclosed data might be most likely to get lost.
One thing is certain for me. I'm far more secure than I ever have been until I adopted Diceware.
I also suppose that the required effort and computing power needed by casual snoops is likely to become ever easier to come by.
0 -
When Reinhold was making his recommendations, there was nothing like PKBDF2, and was working on the assumption that passwords could be tested as quickly as AES keys. I had (erroneously) followed his advice in that first article.
What we have learned since then are the kinds of cracking speeds that are actually achieved. My initial advice was based on extremely pessimistic (from the defenders point of view) guesses about attackers' capabilities. Now that John the Ripper and hashcat actually take on 1Password, we have far better estimates of cracking speed, and so can put things in terms of "how long to crack on such and such system"
This, then, leads to @hawkmoth's excellent point that you need to consider your threats. Is someone going to spend 10 years with a high-end PC trying to crack your Master Password? What resources is an attacker willing to burn to get your Master Password? Only when you've considered that can you make a choice about how strong your Master Password should be.
Cheers, -j
0 -
Jeff—
Thanks for you perspective, as always! Please note that I offered no opinion of my own. :-)
Your Toward Better Master Passwords blog post continues to be a point of reference for many of us. If it does not represent your current thinking, perhaps this should be flagged in situ and not just in discussion threads like this one. If you believe that it no longer represents Arnold Reinhold’s thinking, perhaps a suggestion that he revise his FAQ would be in order.
Two questions for you:
If I were to posit that 7,776 rounds of PBKDF2 equals one Diceware word, would you consider my proposition to be precisely correct, at least in one sense, or would I be oversimplifying matters?
Are OpenPGP private keys protected with PBKDF2 or something of that ilk?
—Ben F
0 -
You (@benfdc) are probably right that specific length recommendations should be updated in light of what we now know of attackers' capabilities and of individuals' security requirement. I'm wondering whether there should be a regularly updated table of crack times. Seems like a good idea.
I like trying to cite original sources. A lot of people today are calling this scheme "XKCD Passwords", but I would really like people to recognize the history. (Also that article of mind was posted before the XKCD comic.) I don't like "revising history" putting in a bunch of "Update: ..." things isn't great either. But sometimes exceptions need to be made.
If I were to posit that 7,776 rounds of PBKDF2 equals one Diceware word, would you consider my proposition to be precisely correct, at least in one sense, or would I be oversimplifying matters?
You would be entirely (but interestingly) wrong. Adding PBKDF2 rounds only adds to time needed to crack. But adding diceware worrds multiplies the time to crack.
Going from 10000 PBKDF2 rounds to 17776 rounds doesn't even double the cracking time. Going from three diceware words to four diceware words multiplies the cracking time by 7776.
So when we are talking about cracking time, adding more to the passprhase multiplies the crack time, while PBKDF2 only adds to the crack time. When we think about these things in terms of bits (which are on a logarithmic scale) the each diceware word adds about 13 bits. But in terms of bits, each additional PBKDF2 round adds fewer and fewer. Going from one thousand rounds to ten thousand rounds is like adding about 3.3 bits. But going from ten thousand to nineteen thousand (also adding nine thousand rounds) adds less than a bit.
So there is no general comparison. If you have few (or no) PBKDF2 rounds, then adding rounds helps a lot. But once you've got plenty, adding the same number of rounds doesn't do much good. If you start with ten thousand rounds, then to get the same effect as you would by adding a single diceware word, you would need to have 7776 × 10000 rounds total. That's more than 77 million.
And I'm going to say this another way as well. Adding diceware words dramatically (exponentially) increases the number of guess an attacker needs to make. Adding PBKDF2 rounds adds linearly to the time needed for each guess.
Are OpenPGP private keys protected with PBKDF2 or something of that ilk?
Yep. Indeed, PBKDF2 is an out-growth of non-open PGP. I believe that passphrases generated today with PGP will use 2000 rounds of PBKDF2. But this is not well documented and navigating the source is tough if haven't been following it all along. And you should all be proud of me that I didn't take this opportunity to launch into a discussion of the history of PGP versions, patents, and export controls.
Cheers,
-j
–-
Jeffrey Goldberg
Chief Defender Against the Dark Arts @ AgileBits
http://agilebits.com0 -
I do admire your restraint, Jeff. :-) More importantly, I admire your selective restraint. I meant to ask whether going from one round of PBKDF2 to 7,776 rounds would be equivalent to adding one diceware word. You took advantage of my lack of clarity to emphasize a very important point.
Regarding a table of crack times, I have a problem with tables that are in the format of the one in @Khad’s first post in this thread. A GPU-based attack on a three-diceword passphrase protected by 25,000 rounds of PBKDF2 will not run through the entire keyspace in 68 days. It will run through the keyspace in 68 GPU-days. If the attacker dedicates 8 GPUs to the task, then the keyspace will be exhausted in 8.5 days.
If someone acquires my 1Password keychain through, say, a breach of Dropbox security, and cares enough about me to try to crack that keychain, it would be the height of folly for me to assume is that a GPU-based attack would be mounted with only a single blade.
0 -
OK. Now I get the question!
Yes, going from one PBKDF2 iteration to 7776 iterations is similar to, but not precisely the same as, adding one diceware word to a password. It's still not "identical to" because it may be off by a constant factor that depends on the ratio of PBKDF2 single round time to single guess time. For example, there might be overhead in a cracker for setting up a new guess that isn't there when just running through PBKDF2 iterations. So I will give you a "yes" if we drop the "precisely the same" part of the question.
The difference is because the PBKDF2 stuff is about the time it takes to make a single guess, while the password strength is about the number of guesses needed. Both of these factor into total crack time, but they are still about different, difficult to compare, things.
And (if you will all forgive the repetition) going from 7776 PBKDF2 rounds to twice that many, 15552, makes a much much smaller difference than the initial move from 1 to 7776. That is, adding one diceware word is like multiplying the number of PBKDF2 iterations by 7776.
The GPU columns in the table from my article on John the Ripper is vague. At the time that it was written there were no GPU implementations. It was based on an off hand comment by Dhiru in his announcement of the the 1Password module for John the Ripper
GPU support is [trivial] to implement and will be done soon (expected
speedup > 100x).
There was no implication about number of GPUs. So in constructing my table, I just picked a 200 time speedup. Note that this was a speedup against a CPU based system that had 8 effective CPUs; so at every point, I was making pessimistic (from the defender's point of view) estimations.
John the Ripper also has a module for the 1Password 4 Cloud Keychain Format, but I haven't actually tested that. Solar Designer says it is really, really slow (as I would expect). hashcat has yet to develop a module for the new format, but as hashcat tends to be faster than JtR at most cracking, I'm waiting for that to really give a guess of speed.
I suppose, I (or someone) should just put together a calculator for these sorts of things, using number of GPUs, number of CPUs, power of each, particular cracking tool used, PBKDF2 rounds, keychain format, and so on. I sort of have parts of those in the spreadsheet that I used to create those tables, but that is most certainly not fit for public consumption.
What I'd really like to see are more benchmarks. But it seems that while both the JtR and hashcat communities are excited about being able to target 1Password, there hasn't actually been a lot of actual cracking attempts. This is a good thing (it means that there haven't been lots of cases of 1Password data being captured). But that good news has a stormy lining of a lack of any real world data on how these stand up. We really are stuck with extrapolating from a very very small handful of data points.
So really, all of our calculations are very rough "back of the envelope" sort of things. The data that we have is rough. The assumption of linear extrapolation of crack time is reasonable, but hardly precise. These are really rough calculations based on only a few real data points.
I try to compensate for that by always erring in favor of the attacker when creating those tables. I round numbers in a way that make for a stronger attacker. So where I measured 4200 guesses per second, I created the table using 5000. Similarly, I reported the time to go through half of the possible passwords.
0 -
Simple "toward better master passwords" advice:
Add one diceword to whatever you have been using before now, and your password will become 7,776 times stronger than before!
Now here is a paradox for you. Can you make your password 15,552 times stronger than before if you flip a coin to decide whether to tack on your new diceword at the beginning or at the end of your existing password? Intuitively the answer should be yes. But if your original password was generated via diceware, then it seems to me that the answer is no!
0 -
I would assume it is immaterial whether you add a new diceword to the beginning or the end of your current master password, but I don't think I can clearly articulate why I think so.
I would further assume that if you really want all the benefits of Diceware, you really should find a random way to decide what position your new word occupies, including all the internal ones. So for a password with four dicewords, there five possible positions for the new word: beginning, end, and three internal boundaries between the existing words. You probably ought to pick among those by a truly random process. So you shouldn't toss a coin, you probably should roll a die. (I don't know what you do if you roll a six - probably throw again.
I may just have argued the opposite of my initial instinct. I'm certainly out of my expertise! :)
0 -
Now here is a paradox for you. Can you make your password 15,552 times stronger than before if you flip a coin to decide whether to tack on your new diceword at the beginning or at the end of your existing password?
You are both correct in that the answer is "no".
It's because the decision (no matter how randomly made) to pre-pend or append the word doesn't change the number of possible passwords you could end up with. You could flip a coin to decide whether to use red dice or white dice, and that coin flip wouldn't make a difference either.
The interesting question is why this works at this way for this case, but if you were adding something that wasn't a diceware word, say a single digit, the coin flip to pre-pend or append would add a bit.
The solution to this paradox requires separating the process of how you get from one password to another (adding this or that) to thinking in terms of simply of the number of distinct possibilities. It is extremely useful and helpful, in general, to talk about "doing X adds N bits of entropy", but we need to recognize that the kind of effect that "doing X" has depends on what you are starting with.
Let's consider an example. Suppose you've got a password scheme that is this:
- Passwords are 7 characters long
- 1st character is uppercase Roman alphabet letter
- 2nd character is lowercase Roman alphabet letter.
- 3th character is uppercase Greek letter
- 4th character is lowercase Great letter
- 5th is arabic letter
- 6th is uppercase Cyrillic
- 7th is lowercase Cyrillic
(I don't know the letters number of letters of all of those alphabets; let's pretend they are all 25)
That scheme will give us just 25^7 (32 bits if each particular element is chosen truly randomly). But now suppose we say "do X" to that scheme, where "X" is "shuffle". Shuffling these takes us to 44 bits. (175 * 150 * 125 * 100 * 75 * 50 * 25 possibilities)
But now consider a scheme were we say 7 characters long and each character can be any letter from any of those alphabets. 175^7 possibilities. If we say "shuffle that" for this second scheme it has no effect at all. Shuffling does not add to the number of possible outcomes in the second case. That's because order was already unrestricted in the second cade.
So this is a just a long way of saying that the effect of "do X to Y" really depends on the relationship between X and Y.
We know that for password strength we can always say what effect "append X" will have. And we know what effect "prepend X" will have. But we don't know what effect "append or prepend X" will have. It depends on the relationship between X and what you start with.
0 -
And now that I've posted that, I think of a simpler example:
Suppose you've got a password that is all lowercase letters. The effect of "append or prepend a random lowercase letter" will increase the possibilities by 26 (not 52). But the effect of "append or prepend a digit" will add 20 possibilities (not 10).
0 -
Now that you've posted that, my head is spinning. This makes me really glad that you folks are on my side.
0 -
I am thankful every day that Jeff is on our side. :)
0 -
@jpgoldberg wrote:
You (@benfdc) are probably right that specific length recommendations should be updated in light of what we now know of attackers' capabilities and of individuals' security requirement.
The 1P4/Mac setup documentation directs users to your Toward Better Master Passwords post. Unless AgileBits comes up with another essay to link to, it seems to me rather imperative that the recommendations in your original post be adjusted to reflect what has been learned since the post was first written.
0 -
The 1P4/Mac setup documentation directs users to your Toward Better Master Passwords post. Unless AgileBits comes up with another essay to link to, it seems to me rather imperative that the recommendations in your original post be adjusted to reflect what has been learned since the post was first written.
I second this recommendation.
In addition, this interesting discussion allows me to bring up a question that has been noodling at the back of my mind since I first installed 1Password and set my password using the advice on this very site:
If we accept that our 1Password password should theoretically stay the same for life, don't we need to consider future increases in cracking speed when considering the strength of our password? My understanding is that 1Password 3.8 and earlier used 1000 iterations of PBKDF. Someone using a four-word Diceware on version 3.8 would have a password that would withstand GPU attack for 58 years, according to the table posted earlier in this thread.
However, let's assume attacks scale linearly with GPU use, and 8 GPUs are used. Let's also assume GPU power roughly doubles in power every 18 months. If my math is right, in 15 years time that same 4-word Diceware with 1000 iterations of PBKDF would take just two days to crack. Five years later it would take an afternoon, and five years after that it would take just minutes.
This doesn't even take into account reasonably plausible breakthroughs which may dramatically alter the equation, such as the use of quantum computing.
If I'm lucky, I could live another fifty+ years on this planet. If I used the same four-word Diceware password, less than half way through my (hoped for) lifespan, my "for life" password would be crackable in minutes. Assuming a doubling in GPU power every 18 months for the next 50 years, I would need a 6-word password with 25K iterations to have a reasonable chance of not being crackable in my lifetime. If I cared about preventing the cracking of my passwords even beyond my death, I would likely need a 7 or greater word password.
Since I don't know what secrets I might accumulate over the next 50 years and have to reasonably presume that there's at least a chance I may have some that I wish to keep beyond the grave, my logical conclusion would be that if I wish to truly keep one password for life, that I should choose a 7 (or greater) word password.
Thoughts? How's my logic?
0 -
I'll update that blog post. Thanks @benfdc and @EnerJi
The other question that @EnerJi raises centers around the difficulty of meeting the ideal of a Master Password for life.
Bits of the future
Moore's law gives the attacker a 1 bit increase (doubling in power) per 18 month. So if it takes d dollars today to creak an n-bit password today, in 18 months the same expense will get you an (n+1)-bit password. It really is easier in this case to talk about things in terms of bits.
So using your numbers, 50 years, corresponds to a 33 bit increase in power for the attacker. So you should find the crack time you are comfortable with today and then add three words (39 bits) to give it at least that same crack time in 50 years. (By the way, this was the thinking behind my initial "7 words" statement. I was aiming for 88-bits for reasons I won't go into now.)
But I don't think that we should be extrapolating 50 years into the future. It's just too far. First of all, I really hope that the "password problem" is solved by then. There should be no need for 1Password (at least for password management). Sure I used to (15 years ago) think that the password problem would be solved by now, but even that history of poor prognosis doesn't deter me from predicting that people won't be using lots of passwords 50 years from now.
It's not just passwords, 50 years is just too far out there to make projections about technology. I'd love it if 1Password today can protect you against the kinds of attacks that will be around in 50 years, but as the Yogi says, "predictions are very hard to make, particularly when they are about the future."
Most people in the information security business aren't willing to talk beyond a 30 year horizon. So let's reduce things to that. That is 20 bits that you need to plan ahead, or two diceware words to add.
A quantum of perspective
We actually know what quantum computers could conceivably do if built for things like searching for cryptographic keys. Using Grover's algorithm they cut the effective bit strength in half. That is the amount of "time" they take is the square root of what a non-quantum system would take. (Grover proved that this is, indeed, the best algorithm.)
There is an extremely important condition for Grover's algorithm to be used. Everything about checking a candidate password must be part of the quantum state. So the all of the PBKDF2 manipulations, the attempted decrypting with the derived key, the generation of password guesses must all be fully part of the quantum processes. When Grover's algorithm is running, it can't interact with non-quantum information. So while I know that there is much that will surprise me, I really don't think that we will see quantum password crackers in our life times.
I expect other developments in quantum computing that will affect cryptography, but not password cracking.
Cheers,
-j
–-
Jeffrey Goldberg
Chief Defender Against the Dark Arts @ AgileBits
http://agilebits.com0



